Magical Power of Quantum Mechanics

Assessing Reactivity with LUMO and HOMO Energy Gap

QM Magic Class | Chapter 25

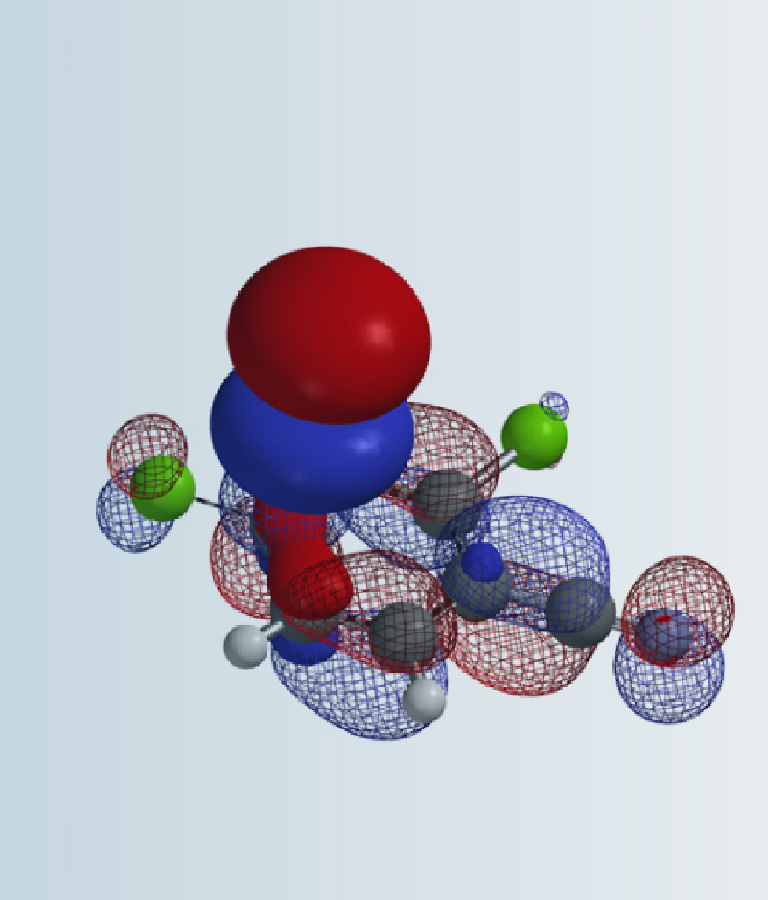
In organic synthesis, we need to pair substrates and reagents of proper reactivity for the reactions to proceed smoothly. For example, halogenation of electron-rich aromatic substrates with N-chlorosuccinimide (NCS) usually works, while for electron-deficient ones, we’ll need to use dichlorohydantoin (DCH) or even trichloroisocyanuric acid (TCCA). DCH and TCCA are stronger chlorination reagents than NCS. How much stronger? Is there a way to quantify the differences?

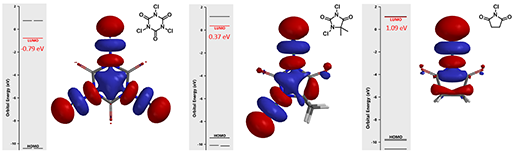
Figure 1. LUMO orbitals and energies of TCCA, DCH and NCS

The calculated LUMO orbitals and energies of TCCA, DCH, and NCS are shown in Figure 1. The LUMO lobes of these reagents are distributed around the chlorine atoms, not on the carbonyl carbons, consistent with the fact that they are halogenation reagents rather than acylation reagents. TCCA has the lowest LUMO energy of -0.79 eV, DCH LUMO has an intermediate energy of 0.37 eV, and NCS has the highest energy of 1.09 eV. These calculated LUMO energy numbers correlate with chemical reactivity of the reagents: the lower the LUMO energy, the more reactive it is as halogenation reagent.

Correlation between LUMO-HOMO energy difference and reactivity

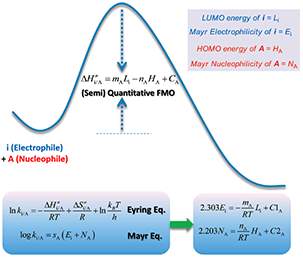
Figure 2. A Frontier Molecular Orbital Theory approach to understanding the Mayr Equation

Why LUMO energy could be used to gauge chemical reactivity? Zhi-Xiang Yu’s group provided a theoretical understanding of the Mayr equation based on frontier molecular orbital theory (FMO) and the Eyring equation of the transition state theory, showing that the nucleophilicity of a molecule is related to the energy of this molecule’s highest occupied molecular orbital (HOMO), while the electrophilicity is related to the energy of the lowest unoccupied molecular orbital (LUMO) of the electrophile (Figure 2)^[1]. In other words, the nucleophilicity and electrophilicity of substrate/reagent can be assessed by their HOMO and LUMO energies, and whether the reaction will proceed or not could be judged by the difference in energy of the orbitals involved in the reactions.

Next, we’ll make use of this LUMO-HOMO energy difference analysis to account for reactivity pattern observed with a set of substrates for Pictet-Spengler reaction.

Analysis of a set of substrates for Pictet-Spengler reaction

Pictet-Spengler reaction is the condensation of β-(hetero)aryl ethylamines with aldehydes or ketones under acidic conditions, followed by addition of the nucleophilic aromatic moiety of the molecule onto the resultant electrophile imine to provide the cyclization product (Figure 3, top).

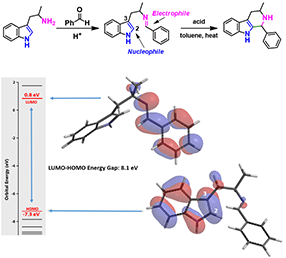
Figure 3. Pictet-Spengler reaction (top) and LUMO orbital, HOMO orbital and energy of imine (bottom)

As illustrated in Figure 3, there are HOMO lobe distributed between C2 and C3 of indole, and LUMO lobe on the imine carbon on the condensation intermediate. Interactions of these orbitals lead to the cyclization observed. Reactivity can be gauged by the energy difference between the LUMO and HOMO orbitals, which is 8.1 eV for the structure in Figure 3. If there is no lobe distributed on HOMO or LUMO at the reaction sites, HOMO-1/HOMO-2 or LUMO+1/LUMO+2 with appropriate lobe distribution should be considered for the energy gap estimation.

Next, we change the substitution position on the indole ring or replace the indole with various aromatic and hetero-aromatic systems, while holding the phenyl imino moiety unchanged. The LUMO and HOMO energies and their differences of this series of imine intermediates are shown in Table 1 (see Figure 4 for their structures).

able 1. LUMO and HOMO orbital energies and their differences

for a series of imine intermediates in Pictet-Spengler reaction

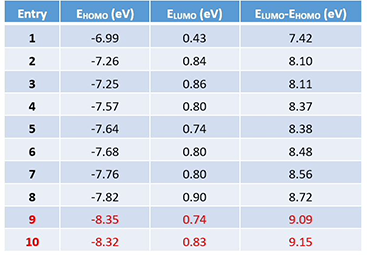
As shown in Figure 4, as the energy difference between LUMO and HOMO gradually increases, higher reaction temperature and/or stronger acid are required for the cyclization to occur^[2]. When the orbital energy difference exceeds the threshold of about 9 eV, the reaction does not proceed under the conditions investigated.

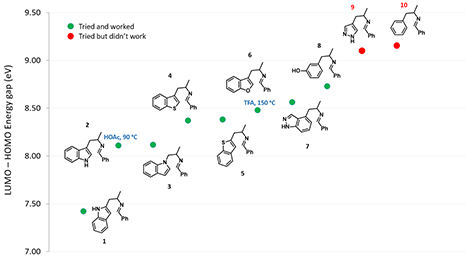
Figure 4. Correlation of LUMO-HOMO energy difference with reactivity in Pictet-Spengler reaction

The above correlation enables us to predict whether a substrate could undergo the Pictet-Spengler reaction or not, simply by comparing the energy gap calculated versus the threshold of 9.09 eV, established with the pyrazole analog 9 and phenyl analog 10, and what cyclization conditions to use by referencing to examples on the Table/Figure.

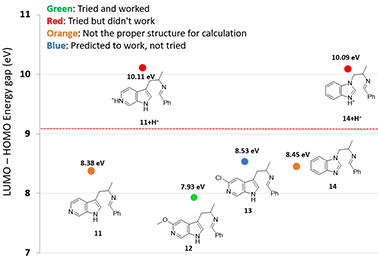
Figure 5. The LUMO-HOMO energy difference was used to predict the reaction activity of different substrates

(Energy differences: 11, 12, 13 are based on LUMO and HOMO; 11+H⁺ is based on LUMO+1 and HOMO-2;

14 is based on LUMO and HOMO-1; 14+H⁺ is based on LUMO+2 and HOMO-3)

For substrates containing basic nitrogen, we also need to consider the pKa of the substrate. For 5-azaindole 11, the LUMO-HOMO energy difference is 8.38 eV, which is within the range where the reaction can occur. However, the cyclization did not proceed and literature search did not reveal any successful example. We reasoned that under the TFA acidic reaction conditions, the pyridyl nitrogen is protonated (Fig. 5, pyridine pKa ~ 5.2), and the LUMO-HOMO energy difference for 11+H⁺ is actually 10.11 eV.

This challenge was readily resolved by introducing a methoxy or chloro substituent adjacent to aromatic N to lower its basicity (pKa of 3.2 and 0.7 for 2-MeO- and 2-Cl pyridines, respectively)^[3]. The LUMO-HOMO energy differences of MeO-substituted substrate 12 and Cl-substituted substrate 13 are estimated to be 7.93 eV and 8.53 eV, respectively. We decided to prioritize the synthesis of the methoxy product first because the LUMO-HOMO energy difference of 7.93 eV is further away from the threshold of 9.09 eV, and successfully synthesized the methoxy Pictet-Spengler reaction product. The methoxy group was converted into triflate and hydrogenated to provide the 6-azaindole product^[4]. The triflate intermediate also enables us to establish further SAR in that part of the inhibitors.

A similar hurdle was anticipated for the benzimidazole substrate 14+H⁺ with an estimated orbital energy gap of 10.09 eV. This alerted us to design an alternative synthetic route for the target^[4].

especially suitable for reactions that have a useful number of examples for correlation. It is worth noting that this method is very useful when the electronic effect is the main driving factor for the reaction, and requires us to choose the proper orbitals, with lobe at the reaction sites, for energy gap estimation. Potential steric interactions may require special attention.

Building on What We Just learned

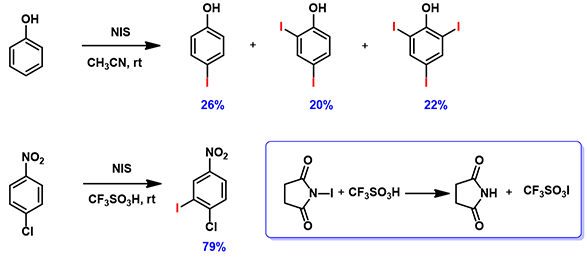
Figure 6. Iodination of phenol and 4-chloronitrobenzene

Reaction of phenol with N-iodosuccinimide (NIS) readily proceeds to provide a mixture of mono-, di- and tri-iodinated products^[5]. However, iodination of 4-chloronitrobenzene with NIS proceeded only in the presence of trifluoromethanesulfonic acid^[6]. It is reasoned that trifluoromethanesulfonic acid reacts with NIS to generate iodine(I) trifluoromethanesulfonate, which is the active species for the halogenation (Figure 7). What reagent will you choose to iodinate 1,2,3-trifluoro-4-nitrobenzene? And will halogenation occur at C-5 or C-6 position? ^[7]

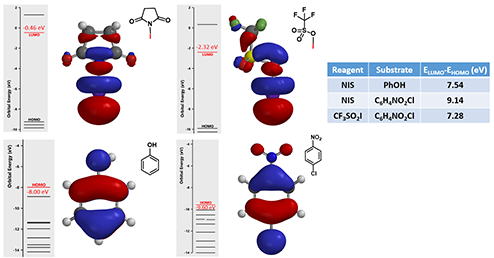
Figure 7. LUMO orbitals of NIS and CF3SO3I and HOMO orbitals of phenol and 4-chloronitrobenzene with corresponding energies

References:

[1] L.G. Zhuo, W. Liao, Z.X. Yu, Asian J. Org. Chem. 2012, 1, 336.

[2] A. Yokoyama, T. Ohwada, K. Shudo, J. Org. Chem. 1999, 64, 611.

[3] https://www.chem.wisc.edu/areas/reich/pkatable/pKa_compilation-1-Williams.pdf

[4] M.K. Jackl, I. Kreituss, J.W. Bode, Org. Lett. 2016, 18, 1713.

[5] P. Bovonsombat, J. Leykajarakul, C. Khan, K. Pla-on, M.M. Krause, P. Khanthapura, R. Ali, N. Doowa, Tetrahedron Lett. 2009, 50, 2664.

[6] G.A. Olah, Q. Wang, G. Sandford, G.K. Surya Prakash, J. Org. Chem. 1993, 58, 3194.

[7] Tips: Calculate for HOMO map and HOMO-1 map of 1,2,3-trifluoro-4-nitrobenzene.

This article is written and edited by Dong Pan, Wenfeng Liu, Tommy Lai, Tao Wang, Yongsheng Chen, John S. Wai