QM有机化学课堂

QM在多卤素底物连续偶联反应中的应用

QM魔法小课堂 | 第五章

我们在前面的QM小课堂知晓了LUMO及LUMO Map的概念，并通过实例初步了解和学习了它们在有机合成中的应用。本章节我们将介绍运用前面所学内容，为多取代杂环分子设计合适的合成路线。

如何从原料(1)快速合成目标分子(4)？

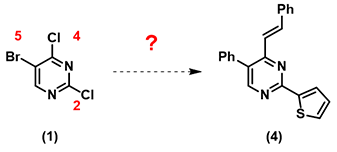
如果起始原料是多卤代的苯环，我们知道反应一般会遵循I > Br > Cl这个排序进行，但杂环体系中的多卤代底物就充满了不确定性。

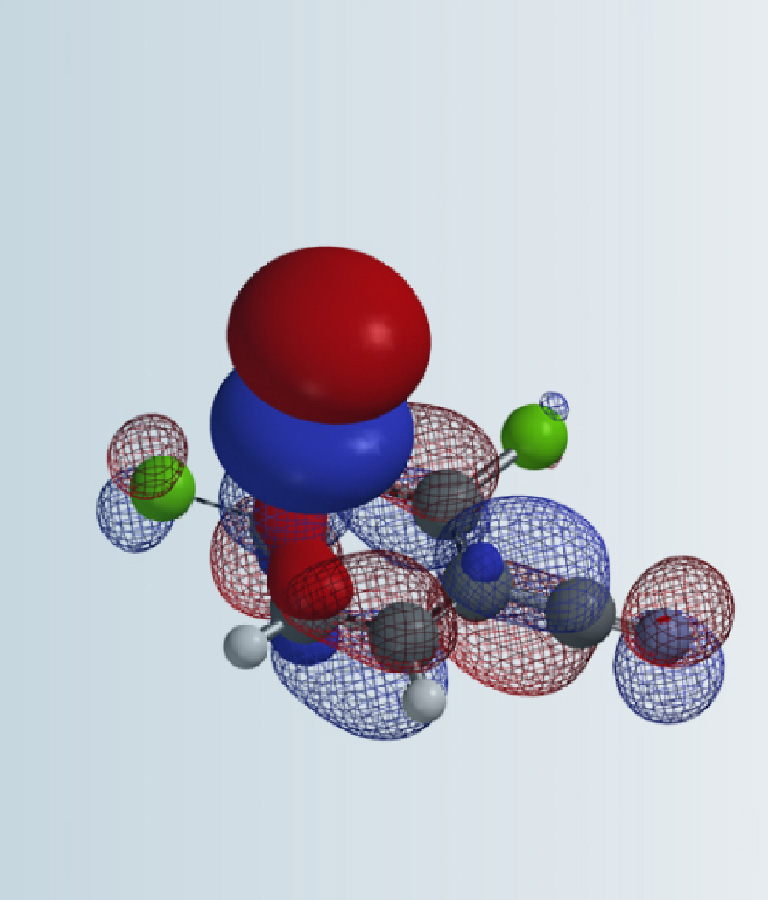
对于底物（1），2, 4, 5 位都为卤素，哪个位点优先引入取代基团呢？一般在 Pd[0]催化 C-X 键交叉偶联反应中，我们可以将 Pd[0]看做亲核试剂，它会优先进攻多个 C-X 键中具有较大 LUMO lobe 的碳。首先我们计算原料（1）的 LUMO：

图 1 可知，LUMO 图示意只有 4-Cl 的碳有很明显的 LUMO lobe。因此，我们在钯催化下，并控制好反应温度在 70 °C，底物（1）可以与锡试剂 A 反应，选择性生成 C-4 位烯基化的化合物（2）：

随后我们计算化合物(2)的LUMO（图 2）：

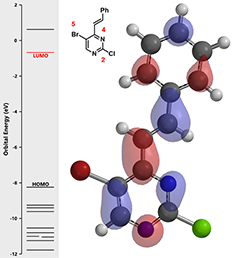
图2. 化合物(2)的LUMO示意图

嘧啶2位和5位的碳均没有明显的LUMO lobes，我们进一步参考LUMO+1的轨道能级示意图：

图3. 化合物(2)的LUMO+1示意图

LUMO+1 的示意图显示嘧啶 LUMO lobe 在 C-2 位和 C-5 位上（图 3），但二者差别不明显。那么此时你是否认为我们要随机试验，撞大运了呢？答案是当然是 NO！山人自有妙计！

这里我们再介绍一个小技巧：计算C-X键的红外（IR）的伸缩振动频率来预测区域选择性。伸缩振动频率相对低的C-X键，该键键能越弱，越容易断裂。

我们打开计算工具，计算化合物(2)中嘧啶2位和5位C-Cl键和C-Br键的红外线伸缩振动频率（图 4）：

图 4. 化合物（2）的 LUMO+1 示意图和计算的红外伸缩振动频率

我们可以很直观的做出比较，5 位 C-Br 键（1165 cm-1）比 2 位 C-Cl 键（1191 cm-1）的键能弱，更易发生氧化加成反应，实现嘧啶 5 位基团的引入。值得注意的是，起始原料（1）的最低未占轨道能量为 -0.21 eV，化合物（2）的 LUMO+1 能级的能量为 0.62 eV，这就要求我们要提升反应体系的温度保证反应顺利进行。在相同催化体系下，升温至80 °C，化合物（2）与锡试剂 B 反应生成产物（3）。

最后一步反应，化合物（3）的 C-2 位没有 LUMO lobe，进一步考察 LUMO+1，其轨道能量比化合物（1）和（2）更高些，约为 0.70 eV（图 5）。

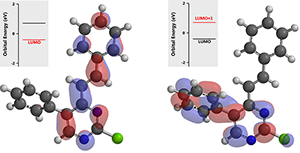
图 5. 化合物（3）的 LUMO（左）和 LUMO+1（右）示意图

这就需要再进一步提高反应强度，升高体系温度至 100 °C，可以成功得到 C-2 位芳基化的终产物（4）。

看完整个流程，您是否发现我们可以尝试在不改变催化剂和溶剂等条件下，仅仅通过改变反应温度，不同阶段加入不同的定量锡试剂，中间步骤不经过纯化，通过一锅法实现三个基团的顺序引入呢？

有没有超简单的感觉？提前计算一下，比没思路的盲目尝试节省大量的时间和精力！

总结一下，通过 QM 计算我们优先考虑各反应位点 LUMO 和 LUMO+1 lobe，如果不能明显判别，再继续计算红外伸缩振动频率比较，通过评估各活性官能团参与反应的活性顺序，在一个相对普通的反应条件下，设计出一条简洁且经济的合成路线。

小试牛刀

本期我们也留了一个案例供大家思考：

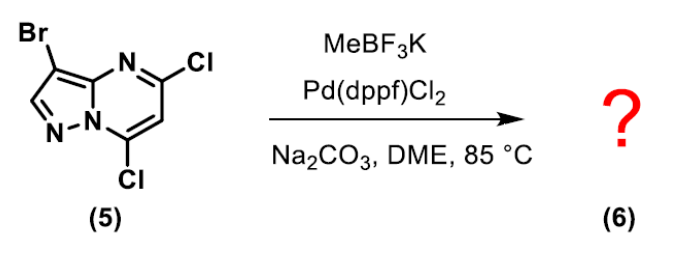
你能试着按上文所述的思路，参考如下所示的QM计算数据示意图给出一个合理的预测么？

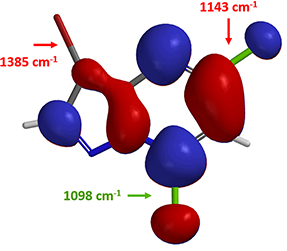
引入一个取代基后，第二个取代基会在哪里发生反应呢？

参考文献：

[1] W. Hehre and S. Ohlinger, A Guide to Molecular Mechanics and Quantum Chemical Calculations. Irvine, CA, USA: Wavefunction, Inc., 2003.

[2] J.A. Joule & K. Mills, Heterocyclic Chemistry 4th Ed. Malden, MA, USA: Blackwell Publishing Ltd., 2000; pp 202.

[3] R.M. Badger, J. Chem. Phys. 1934, 2, 128.