 选择语言
选择语言

各位好学的小伙伴们,我们又回来啦!
去年秋天,我们推出了《QM魔法小课堂》系列文章,为大家介绍如何利用QM计算来可靠地预测有机化学反应结果,迄今已陆续推送了七篇小文章。
仔细听课的同学会发现,之前的计算基本只涉及杂环底物。我们在日常实践中发现,有时仅计算底物的HOMO/LUMO还不够,需要进一步模拟反应过渡态,计算反应活化能,才能对反应选择性做出准确的预测。因此,从下期开始,会为大家介绍一些相关的应用实例。
不过今天,我们先来上一堂理论课,回顾几个支撑反应过渡态计算的重要理论。
1889年• 阿伦尼乌斯公式(Arrhenius Equation)
一个化学反应为什么可以发生?反应的速率为什么有快有慢?反应的选择性又是由什么因素决定的?1889年,阿伦尼乌斯最先提出了一个经验公式,总结了反应速率与温度之间的变化规律:
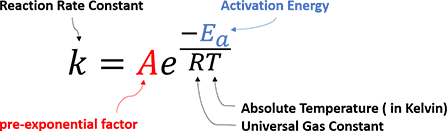
图1.阿伦尼乌斯经验公式
这个公式相信大家都非常熟悉了。阿伦尼乌斯提出,反应物分子需要获取一定的能量,转化成活化分子,互相碰撞才能发生反应,他将这个能量称为活化能Ea。通过测量反应速率随温度的变化,就可以计算出反应所需的活化能。这个公式完全从实验测量所得的参数出发,其适用范围很广。但是在微观层面,对于反应发生的具体过程,以及这个公式内的特征参数,阿伦尼乌斯并没有给出详细的描述或解释。
在这之后的几十年里,科学家们提出了很多理论,试图进一步解释阿伦尼乌斯公式,希望能直接从理论出发预测反应速率常数等。这其中,亨利·艾林等人于1935年提出的过渡态理论以及艾林公式(Eyring Equation),给出了一个更为精细的,基于统计热力学与量子力学的公式:
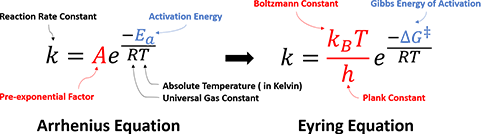
图2.阿伦尼乌斯经验公式与艾林统计热力学公式的对应关系
这个公式与阿伦尼乌斯公式的数学形式非常相似,但是它针对阿伦尼乌斯公式里的经验参数,给出了更具体的物理意义:
1. 反应活化能: 艾林等人认为,反应不是通过简单碰撞就能发生的,而是需要反应物分子之间形成过渡态络合物。反应物分子达到过渡态所需要的能量,即为活化能。另外,过渡态理论中还引入了热力学概念,用吉布斯活化自由能ΔG‡指代反应活化能,以考虑焓变与熵变。而对于复杂反应,每一个过渡态都有相对应的活化能。
反应物分子在接触时,分子内部结构会相互作用,整个系统的势能也会不断变化。以图3为例,反应物X以稳定的构象处于反应势能面的低谷处,经由不同的反应路径,形成高能量的过渡态,数学定义上称其为马鞍点(saddle point),然后分解得到不同产物。
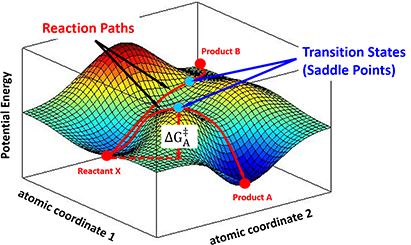
图3. 反应物X通过不同反应路径生成产物A或B的反应势能示意图
2. 指前因子A(pre-exponential factor): 与分子振动以及过渡态的熵变有关。
过渡态理论最大的贡献,在于利用统计热力学,为宏观层面观察所得的阿伦尼乌斯经验公式,提供了一个微观层面的数学模型以及物理意义。理论上来说,根据分子的微观物理量,比如振动频率、质量等,通过构建反应势能面,就可以计算、预测活化能,找到过渡态。
在实践中,构建反应势能面非常困难,但“反应过渡态”这一概念却为大家普遍接受。1955年,乔治·哈蒙德提出了一个迄今都意义深远的假说,其原文如下:
“如果一种过渡态和一种不稳定的中间体具有连续递变的关系,而且它们的能量差别不大,那么它们之间的转变只涉及结构上微小的变动。”
进一步引申,在单步的化学反应中,如果是高度放热的反应(图4左),因为反应物能量远高于产物,那么过渡态的能量就会近似于反应物,其结构也会更类似于反应物;而在吸热反应中(图4右),产物的能量高于反应物,过渡态能量则更接近于产物,所以结构也会更像产物。
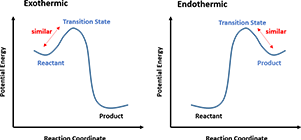
图4. 哈蒙德假说下过渡态结构与反应物、产物的关系
反应过渡态络合物的存在时间极短,在皮秒(10-12)级别,转瞬即逝,实验中难以捕捉。因此,哈蒙德假说最大的意义,是为我们提供了过渡态的结构模型。在这一假说的基础上,我们可以以反应物或产物为基础,推测过渡态的结构,直接从结构出发,计算达到反应过渡态所需要的能量。
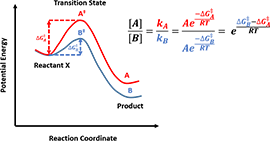
图5. 利用反应过渡态能量差值计算反应产物比例
对于化学合成中经常遇到的区域选择性问题,我们可以通过比较不同过渡态的能量,预测不同产物比例。以图5的反应进程为例,反应物X可以经由反应过渡态A‡和B‡分别生成产物A和B。在动力学控制的化学反应中,产物A和B的比例正比于它们各自的反应速率kA与kB。这是今后的章节中,我们预测反应产物比例的主要依据。而在热力学控制的化学反应里,由于反应产物达到平衡,可以直接通过计算产物与反应物的势能差之比,预测产物的比例。
由于反应过渡态涉及到断键与成键的过程,而量子力学则是直接对分子内各电子的分布进行计算,与分子是否成键无关,因此,利用QM工具进行过渡态结构的模拟,有更大概率能接近真实状态,解决实验无法捕获过渡态络合物的难点,还能进一步通过研究过渡态性质,对反应结果做出预测。
回溯这些理论的诞生,我们会发现这些耳熟能详的基本概念,凝聚了很多代化学家们的心血。从最早的实验观察与宏观测量,到提出微观层面的“反应过渡态络合物”,再从能量相近的反应物或产物,推测“反应过渡态”的结构,一步步探究化学反应的发生、进程、与机理。
现在的我们,正是站在巨人的肩膀上。将前线轨道理论、哈蒙德假说,与日益成熟的量子计算工具结合起来,通过对反应物HOMO与LUMO的计算,和过渡态的模拟,辅助化学反应预测,解决日常合成路线设计里的问题,相信这也终将会成为未来的趋势!
本文由石谷沁、王守亮、王秋月、卫小文编撰。
参考文献:
[1] Fu Xiancai et al (2006). Physical Chemistry. Beijing, P.R. China: Higher Education Press.
[2] Y. Wang (2014). First principles process planning for computer-aided nanomanufacturing In J. G. Michopoulos, C. J. J. Paredis, D. W. Rose, J. M. Vance (Ed.), Advances in Computers and Information in Engineering Research, Volume 1. New York, NY, USA: ASME Press.
[3] H. Eyring. J. Chem. Phys. 1935, 3, 107-115
[4] G. S. Hammond. J. Am. Chem. Soc. 1955, 77, 334-338